Resolviendo el cubo de Rubik
¡¡IMPORTANTE!! Si vais a ver el tutorial en un MAC, abridlo con Safari. Da problemas de carga con Firefox y Chrome.
Índice de
contenidos
- A. Introducción
- B. Estructura del cubo de Rubik
- C. Notación
- D. Método
- 1. Cruz
- 2. Primera capa (esquinas)
- 3. Completar segunda capa (aristas)
- 4. Orientar última capa:
- 5. Permutar (colocar) última capa:
- E. ¿Y ahora qué?
- Hardware: Portátil Toshiba Portégé R500 (Intel Core2 Duo U7600 1.20 GHz, 2GB RAM)
- Sistema Operativo: Windows 7 Ultimate
- Mozilla Firefox 3.6.9
A. Introducción
Este año se celebra el 30 aniversario del puzzle
más famoso de la historia: el cubo de Rubik. Para celebrarlo
y aprovechando el final del verano, este tutorial no tratará
sobre tecnología, sino sobre cómo resolver el
dichoso cubo.

En realidad Ernö Rubik, escultor y profesor de arquitectura
húngaro, inventó su cubo ya en 1974, pero fue en
Febrero de 1980 cuando llegó por primera vez a
jugueterías fuera de Hungría. Desde entonces, se
estima que se han vendido más de 350 millones de unidades en
todo el mundo.
Obviamente hay miles de tutoriales y vídeos sobre
cómo resolver el cubo de Rubik en Internet, pero vamos a intentar
aportar un poco más, viendo un método de
resolución en el que:
- comprendamos la estructura del cubo y
cómo se mueve - nos obligue a pensar un poco durante el
proceso - minimice la necesidad de memorizar
algoritmos - y nos pueda servir de base para
aprender métodos más avanzados de
resolución rápida, resolver cubos de orden mayor
(4×4, 5×5, …) y otros tipos de puzzles secuenciales
(pyraminx, megaminx, …)
(necesitaréis Java (JRE) para poder ver correctamente el
tutorial)
Antes de nada, vamos a empezar por conocer un poco más el cubo.
B. Estructura del cubo de Rubik
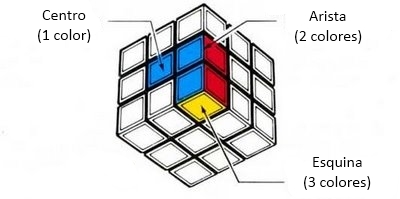
El cubo de Rubik consta de 26 piezas, con un core central: 6 centros, 12 aristas
y 8 esquinas:

Los centros están unidos a la pieza central, lo que nos
lleva a nuestra primera propiedad importante: los centros NO se mueven.
Es decir, siempre están en la misma posición
relativa:

Así, el centro de cada cara será el que marque el color de la misma. En la configuración estándar de colores, eso
significa que las caras blanco-amarillo, naranja-rojo y azul-verde
siempre serán opuestas:
(podéis mover el cubo si queréis verlo mejor)
Los centros tendrán un solo color, mientras que las aristas 
tendrán dos y las esquinas  tres.
tres.
Eso nos lleva a nuestra
segunda propiedad: las pegatinas no se mueven individualmente, sino que
son las piezas las que debemos colocar. Así pues, no
servirá de nada colocar bien un lado de una esquina si los
otros dos no están en su posición correcta: la
pieza estará mal colocada.
En este sentido, distinguiremos dos propiedades en las aristas y
esquinas: posición y orientación. Es decir, una
pieza puede estar colocada en su posición correcta, pero mal
orientada. Así, una arista presentará dos
posibles orientaciones: correcta o incorrecta; mientras que una esquina
tendrá tres: correcta, girada en el sentido de las agujas
del reloj, o en el contrario.
La tercera propiedad importante es que las piezas no son
independientes, lo que introduce ciertas restricciones
matemáticas: por ejemplo, no puede haber una
única pieza mal orientada (al menos 2), o sólo
dos piezas mal colocadas (al menos 3). No profundizaremos
más en este concepto de momento, pero sí lo
emplearemos durante la resolución. Es además
importante resaltar que si desmontamos el cubo y lo volvemos a montar
al azar, puede que lo hagamos en una configuración
irresoluble.
C. Notación
Para ayudar en la memorización (y sobre todo en la comunicación)
de los algoritmos, existe una notación
estándar para indicar los movimientos.
Las caras se nombran por su posición relativa,
según miramos el cubo y en inglés:
F-Front, B-Back, R-Right, L-Left, U-Up, D-Down

y los movimientos se indicarán con la letra de la cara que
se gira:
- R – La cara derecha se gira 90º en sentido horario
(si miráramos de frente a dicha cara) - R’ – Giro de 90º en sentido antihorario
- R2 – Giro de 180º (obviamente, da igual el sentido,
aunque también podemos indicarlo – R2’)
(hay también notación para movimientos de 2
capas y de cubo completo, pero no los emplearemos en este tutorial).
Aquí tenéis los movimientos representados con el
applet que usaremos a lo largo del tutorial (el applet es un excelente trabajo de Josef Jelinek):
 Ver siguiente paso
Ver siguiente paso
 Ver toda la secuencia
Ver toda la secuencia
 Restaurar
Restaurar
el cubo vosotros, tanto giros de cara (botón izquierdo) como
movimientos de todo el cubo (shift+botón izquierdo o
botón derecho). Aprovechad para familiarizaros un poco con él.
Y una vez dadas estas nociones básicas, vamos a comenzar con
el método de resolución.
D. Método
Vamos a emplear un método de resolución por
capas, basado en el método Fridrich (probablemente el
método más popular de speedcubing) pero muy
simplificado, con pocos algoritmos y con los pasos desglosados.
Los pasos que daremos para la resolución del cubo de Rubik
serán los siguientes:
Cada uno de los pasos no afectará a lo conseguido en los
anteriores, si bien en los pasos de la última capa, como es
obvio, tendremos que deshacer brevemente el resto del cubo durante los
algoritmos.
Jessica Fridrich, consta de 4 pasos: cruz, 2 primeras capas (nuestros
pasos 2 y 3 juntos), orientar última capa (un solo paso) y
permutar última capa (un solo paso). Un buen speedcuber los
llevará a cabo aproximadamente en 2 seg + 8 seg + 4 seg + 4
seg, para un total de menos de 20 segundos. El record actual de
resolución del cubo de Rubik está en poco más de 7
segundos.
Podéis seguir los pasos en los applets que se incluyen, pero
lo ideal sería que además siguierais el tutorial con un cubo en la
mano (podéis conseguir uno cutre en cualquier chino, aunque
os costará bastante girarlo. En Toys ‘R’ Us podéis encontrar el oficial, así como una copia más barata… e incluso mejor).
También
podéis descargar e instalar el excelente SW de
simulación de GabbaSoft
(que además os
tomará tiempos y os permitirá jugar con otras
dimensiones: 2×2, 4×4, 5×5, …):
Como alternativa, os dejo también un applet a tamaño grande para seguir el tutorial en otra ventana:
Applet
En cualquiera de los casos, antes de resolver vuestro cubo, deberéis empezar por mezclarlo, si no lo estaba ya. Una vez hecho esto, empezamos…
1. Cruz – Cross
Elegiremos siempre un color para la cruz (lo cual nos fijará
también el color de la última cara – la opuesta) para
facilitar el reconocimiento de las piezas y la solución. En
nuestro caso haremos la cruz en blanco (es lo más habitual, aunque obviamente podéis elegir cualquier color).
El objetivo será obtener el siguiente estado:
Como vemos, tenemos que colocar correctamente las aristas de la primera
capa, tanto respecto al centro de la misma, como respecto a los centros
de la segunda capa (recordad lo que hablábamos de pensar en
piezas, no en pegatinas). Por ejemplo, esta posición, aunque
las pegatinas blancas estén en su sitio, es incorrecta y no
podríamos progresar desde ella:
Este paso será completamente intuitivo, así que
os dejo solos. ¡Suerte!
cómodo (al comienzo probablemente en la cara U)
Antes de iniciar el siguiente paso giraremos el cubo para situarla en D
(más adelante conviene que os acostumbréis a construirla directamente en D).
2. Primera capa (esquinas) – F2L (First 2 Layers)
Una vez conseguida la cruz, vamos a completar la primera capa,
colocando las esquinas en su sitio:
Nuevamente, deberíais ser capaces de llevarlo a cabo solos.
Sin embargo, aquí sí voy a dar unas pistas para
el que se bloquee.
-
Esquina en capa superior, con la cara blanca NO hacia arriba:
Colocamos la pieza sobre el hueco que debe ocupar, giramos en el
sentido marcado por la cara blanca, llevamos la pieza a la
posición superior anterior y la bajamos. Casi mejor con un
ejemplo, ¿verdad?: -
Esquina en capa superior, con la cara blanca hacia arriba:
Nuevamente colocamos la pieza sobre el hueco a ocupar (para no afectar
a otras esquinas) y modificamos su orientación para poder
luego aplicar el caso anterior:
Si la esquina está en la capa inferior, simplemente
colocamos otra esquina en su lugar, lo que la llevará a la
capa superior:
3. Completar segunda capa (aristas) – F2L (First 2 Layers)
El objetivo a alcanzar es el siguiente, las dos primeras capas
correctas:
Otra vez podría ser intuitivo. De hecho, en Fridich, el paso
anterior y éste suelen realizarse a la vez, colocando
parejas esquina – arista (es lo que se denomina F2L).
Vamos sin embargo a ver los dos casos posibles. Suponiendo que la
arista esté en la última capa, la hacemos
coincidir con su centro correspondiente de la segunda capa. Puede quedar en 2
posiciones respecto a la posición objetivo:
-
Izquierda:
-
Derecha:
Para memorizarlos, podéis verlo como:
- alejar la arista de la esquina
- subir la esquina a la capa superior (girando la cara opuesta a donde está ahora la arista)
- llevar la esquina hacia el lado donde está la arista y reconstruir la cruz
- volver a colocar la esquina como en el paso 2, recogiendo la arista por el camino.
orden en cada uno: URUR’ U’F’U’F y
U’F’U’F URUR’
Nuevamente, de modo similar a como hacíamos en el paso 2, si
la arista está en la capa central simplemente colocamos otra
arista en su lugar, lo que la llevará a la capa superior:
4. Orientar última capa – OLL (Orient Last Layer)
Vamos por último a enfrentarnos a la última capa,
y aquí ya no habrá más remedio que
usar un poco la memoria. Trataremos de que sea lo mínimo
posible, más que por el esfuerzo, para que podáis
resolver el cubo de Rubik no sólo hoy, sino también dentro de un mes.
Introduciremos por tanto el concepto de algoritmo, que es simplemente
una secuencia de movimientos que produce un resultado controlado en el
cubo. Es decir, mueve un grupo de piezas de una determinada forma, pero
no afecta a las que ya tenemos situadas.
Dentro de los algoritmos que veremos, una secuencia que utilizaremos
habitualmente será: RUR’U’,
así que conviene que os familiaricéis con ella:
(probad a ejecutarla 6 veces seguidas; el cubo volverá a la
posición inicial).
El objetivo de este paso es solamente orientar la última
capa, es decir, lograr que el lado amarillo (si hicisteis la cruz en
blanco) de todas las piezas esté en la cara que le
corresponde, la superior. Así pues, NO colocaremos
aún las piezas, sólo las orientaremos:
Comenzaremos por las aristas (en Fridich puro, nuevamente, se
haría en un solo paso).
4.1. Orientar aristas
Podemos encontrarnos con tres casos posibles:
-
Aristas opuestas correctas:

Ejecutaremos el siguiente algoritmo, que contiene la secuencia que
vimos anteriormente. Debemos ejecutarlo con las piezas correctas
paralelas a la cara F:F RUR’U’ F’
-
Aristas adyacentes correctas:

Ejecutaremos el siguiente algoritmo, muy similar al anterior (sólo cambiamos el orden de Rs y Us). En este
caso, lo ejecutaremos con las piezas correctas en la esquina posterior
izquierda:F URU’R’ F’
-
Ninguna arista correcta:
Necesitaremos realizar ambos algoritmos, en el orden que
queráis (al ejecutar uno de ellos, obtendréis
como resultado la posición de partida del otro):
Una vez obtenida la siguiente situación:
vamos a ocuparnos de la orientación de las esquinas.
4.2. Orientar esquinas
El algoritmo de orientación de esquinas que veremos NO
afecta a la orientación de las aristas. Sin embargo, los
anteriores de aristas sí afectaban a las esquinas. Por eso
es importante ejecutar los pasos SIEMPRE en el orden marcado.
posteriores tampoco modificarán las orientaciones de las
piezas, y nuevamente los de colocación de aristas no
afectarán a las esquinas. Ninguno es aplicable en el orden
contrario.
Así pues, nuestros pasos siempre serán:
- orientar aristas
- orientar esquinas
- permutar esquinas
- permutar aristas
(esto es consecuencia de los algoritmos que empleamos. Si
utilizáramos otros, podríamos permutar
indistintamente aristas o esquinas primero, pero el objetivo del
tutorial es emplear la menor cantidad de algoritmos y lo más
sencillos posible)
Y después de este rollo, vamos ya con nuestras esquinas. El
objetivo será obtener toda la última capa
orientada:
Emplearemos un solo algoritmo, por lo que es posible que debamos
aplicarlo hasta 3 veces. El algoritmo en cuestión provoca el
giro horario de 3 esquinas, manteniendo la frontal izquierda como
estaba (como véis también desplaza las esquinas, pero eso no nos importa ahora).
RUR’U RU2R’
(al girar una esquina en sentido horario, ésta
pasará por los estados correcto -> horario ->
antihorario -> correcto)
Distinguiremos 3 casos de ejecución (como ya vimos al hablar
de las propiedades del cubo, no puede haber una única
esquina girada):
-
3 esquinas giradas:


Colocaremos la esquina correcta en la esquina inferior izquierda y
ejecutaremos el algoritmo una vez, si las esquinas estaban giradas en
sentido antihorario, o dos veces (tras recolocar la esquina) si lo
estaban en sentido horario:(por las restricciones del cubo, si hay 3 esquinas giradas
sólo pueden estarlo en el mismo sentido) -
2 esquinas giradas:



Aquí os voy a hacer pensar un poco. Necesitamos finalizar
nuestro algoritmo con 3 esquinas giradas, para poder aplicar el caso
anterior. Nuevamente por las restricciones del cubo, una esquina
estará girada en sentido horario y la otra en antihorario.En este caso, colocaremos en la esquina no afectada la esquina
orientada en sentido horario. Así obtendremos:- horario -> horario (no afectada)
- antihorario -> correcto
- correcto -> horario
- correcto -> horario
es decir, 3 esquinas orientadas en sentido horario (a las que tendremos
que aplicar otras dos veces nuestro algoritmo).(conviene que intentéis entender la lógica
detrás de esta elección y de la
próxima … o se os olvidará en breve) -
4 esquinas giradas:

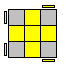
Otra vez por las restricciones del cubo, dos esquinas
estarán giradas en sentido horario y las otras dos en
antihorario.En este caso, colocaremos en la esquina no afectada una de las esquinas
orientadas en sentido antihorario. Así obtendremos:- antihorario -> antihorario (no afectada)
- antihorario -> correcto
- horario -> antihorario
- horario -> antihorario
es decir, 3 esquinas orientadas en sentido antihorario (a las que
tendremos que aplicar una vez más nuestro algoritmo).
5. Permutar (colocar) última capa – PLL (Permute Last Layer)
Una vez que tenemos la última capa orientada, vamos a pasar
a la última fase de la resolución: colocar las
piezas. En esta ocasión comenzaremos por las esquinas.
5.1. Permutar esquinas
Vamos a emplear nuevamente un solo algoritmo en esta fase, que
precisaremos emplear una o dos veces.
El algoritmo en cuestión permuta dos esquinas adyacentes,
las situadas en el lado derecho del cubo (nuevamente
contendrá nuestra secuencia):
RUR’U’ R’F R2U’R’U’ RUR’F’
Como vemos, el algoritmo es bastante más largo de lo que
estábamos acostumbrados. Esto será así
con todos los algoritmos de esta última etapa de
permutación.
etapa en un solo paso, ya que dividir la etapa de
orientación no es tan costoso en movimientos y tiempo. De
hecho, el algoritmo que aquí usamos no sólo mueve
2 esquinas, sino también 2 aristas:
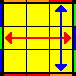
Aplicarlo es obviamente muy simple. Buscad dos esquinas adyacentes bien colocadas
(presentarán dos pegatinas iguales adyacentes) y aplicadlo en las
otras dos (es decir, colocad las esquinas correctas en el lado izquierdo). Si no hay 2 esquinas adyacentes bien, aplicadlo una vez (en cualquier
pareja de esquinas) y las obtendréis.
Una vez tenemos el cubo en este estado,
ya sólo nos queda el último paso: colocar las
aristas.
5.2. Permutar aristas
Una vez más emplearemos un solo algoritmo, que en esta
ocasión provocará el desplazamiento de 3 aristas
en sentido horario. Arista derecha a frente, frente a izquierda e
izquierda a derecha, manteniendo la posterior sin mover. Es decir: 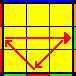
R2U RUR’U’ R’U’ R’UR’
(vemos como una vez más contiene nuestra secuencia
…)
Y otra vez tendremos 3 casos de ejecución (recordemos que no
puede haber sólo 2 aristas desplazadas):
-
3 aristas desplazadas:
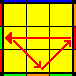

Muy simple, de hecho será el objetivo a alcanzar en los
otros casos. Simplemente ejecutaremos nuestro algoritmo una o dos
veces (con la arista correcta atrás): -
4 aristas – opuestas:
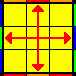
Ejecutaremos nuestro algoritmo en cualquier punto, y obtendremos 3
aristas desplazadas en sentido antihorario, por lo que sólo
tendremos que aplicarlo una vez más (tras colocar la arista correcta atrás): -
4 aristas – adyacentes:
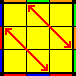
Situaremos la arista permutada con la frontal en el lado izquierdo
y ejecutaremos el algoritmo. Obtendremos nuevamente 3 aristas
desplazadas en sentido antihorario, por lo que sólo
tendremos que aplicarlo una vez más:En este caso, no es excesivamente relevante ejecutarlo en el punto
indicado. Si no lo hacemos así, obtendremos
también 3 aristas desplazadas (aunque en sentido horario),
por lo que sólo supondrá una ejecución
más. En el caso de la orientación de esquinas, si
no sabemos lo que hacemos nos quedaremos bloqueados.
¡¡¡Y felicidades!!!
¡¡¡Habéis resuelto el cubo de Rubik!!!
Espero que os haya gustado la experiencia. Si alguien se ha quedado
totalmente bloqueado (aunque he intentado ser bastante exhaustivo en los ejemplos),
siempre podemos plantearnos intentarlo en vivo en una charla. Simplemente tenéis que decirlo…
E. ¿Y ahora qué?
Si queréis seguir progresando en la resolución del
cubo de Rubik, para hacerlo más rápido y con menos pasos,
el orden lógico de evolución hacia Fridrich
completo sería:
- A. Hacer la cruz directamente en la cara D
- B. Juntar los pasos 2 y 3 – Aprender F2L intuitivo
- C. Aprender algoritmos de orientación de esquinas, para hacer OLL en 2 pasos
- D. Aprender algoritmos de permutación de esquinas cruzadas y resto de aristas para hacer PLL en 2 pasos
- E. PLL en un paso
- F. OLL en un paso
(los pasos A y B son recomendables e intuitivos; los C y D son razonables, pero E y
sobre todo F son más laboriosos).
Si os apetece continuar, sólo tenéis que decirlo
en los comentarios…
Otras posibilidades para continuar son (aunque ya tendría que ser en charlas):
-
Ver pequeñas variantes de solución del 3×3
(supercubos, sheperd, void, ojos cerrados):

-
O avanzar por otros cubos NxN:

-
O cuboides (NxM):


-
O ver variaciones de forma del 3×3:



-
U otros puzzles completamente diferentes en su solución:





Vosotros diréis …



Espectacular.
Que buen rato he pasado.
Gracias Miguel.
Guau, pedazo de trabajo que has realizado!!!
Muy bueno Miguel. 🙂
Google lo ha conseguido resolver en 20 movimientos y fue noticia mundial. Vamos, si superáis eso, ya veo la noticia \\\»empresa PYME española gana a Google en la resolución del cubo de Rubick\\\»… aunque es posible que tu base la hayas cogido de aquí, ¿no?
Si tu origen es diferente al de Google, y no las has cogido como base, me ofrezco voluntario para iniciar un pique con Google, a ver si mejoramos la imagen española en el extranjero hombre, esto es una oportunidad de oro -> jcarmonaloeches arroba gmail punto com, y que tiemble la Nasa
La verdad es que lo que ha hecho Google y lo que planteo yo aquí tienen poco (o nada) que ver 😉
Lo que ha conseguido recientemente un grupo de investigadores, en el que participaba Google y al que Google cedió el equivalente a 35 años de CPU de un ordenador normal, ha sido demostrar que el llamado algoritmo de Dios (el número menor posible de movimientos para resolver el cubo partiendo de una configuración dada) tiene como máximo 20 movimientos (es decir, el número de Dios es 20). Podéis ver más detalles en: http://news.softpedia.com/news/God-s-Number-for-Rubik-s-Cube-Established-151749.shtml, en la página oficial del proyecto: http://cube20.org/ o en un excelente artículo en español: http://eltrasterodepalacio.wordpress.com/2010/08/27/el-cubo-de-rubik-y-el-algoritmo-de-dios/
Con el método que yo os he propuesto para solucionar el cubo, necesitaréis probablemente alrededor de 100 – 120 movimientos para hacerlo (si miráis las applets, sólo el último paso de permutación de aristas ya necesita como mínimo 11), o alrededor de la mitad si aprendierais el mismo método (Fridrich) en su versión más avanzada.
Para que os hagáis una idea de la diferencia de objetivos, un speedcuber empleará unos 60 movimientos en resolver el cubo, y tardará menos de 20 segundos en hacerlo … mientras que los participantes en competiciones de «Fewest Moves» (sí, también las hay) entregarán normalmente una solución para la posición dada de entre 20 y 40 movimientos, para lo cual tienen 1 hora de tiempo.
Ok, gracias por la aclaración. Vaya juguete creó el señor Ernö Rubik, 350 millones de copias vendidas de este invento a nivel mundial…
Hola a todos,
Parece ser que el tutorial da ciertos problemas al abrirlo en un MAC (con Firefox o Chrome). Si lo abrís con Safari os funcionará perfectamente.
como puedo realizar el cubo de rubik en consola utilizando java como es su sintaxis