Índice de contenidos
- 1. Introducción
- 2. Teoría de ML
- 3. TensorFlow
- 4. Instalando y probando
- 5. Ejemplo visual
- 6. Ejemplo en Python
- 7. Referencias
- 8. Conclusiones
1. Introducción
En este tutorial vamos a ver los conceptos básicos de machine learning centrándonos en redes neuronales.
Veremos como TensorFlow puede ayudarnos a conseguir una solución potente y escalable para resolver
problemas complejos de categorización con redes neuronales de aprendizaje profundo.
Este tutorial utiliza el lenguaje de programación Python para los ejemplos. No vamos a explicar cosas concretas del lenguage
pero si aún no lo conoces, no está de más aprender las cosas básicas de un lenguage tan conocido como Python. Podéis empezar por
aquí o por aquí.
Entorno
El tutorial está escrito usando el siguiente entorno:
- Hardware: Portátil MacBook Pro 15′ (2,2 GHz Intel Core i7, 16GB DDR3).
- Sistema Operativo: Mac OS High Sierra
- Entorno de desarrollo: Visual Studio Code
- Software: python, TensorFlow
2. Teoría de ML
Vamos a empezar por un poco de teoría. Explicaremos muy por encima algunos términos
y asuntos que son importantes en el mundo del Machine Learning.
Machine Learnging o «aprendizaje automático» es una rama de la Inteligencia Artificial
que pretende desarrollar las técnicas necesarias para que las máquinas aprendan.
Deep Learning es un término que engloba un conjunto de algoritmos de
aprendizaje profundo. Es un subgrupo de todo lo que abarca ML.
Redes neuronales son un modelo computacional que intenta imitar el comportamiento
de las neuronas de cerebros biológicos. En este modelo se crean varias capas de neuronas
interconectadas con las neuronas de las capas anteriores y siguientes con unos pesos en
los enlaces.
A la unión de una neurona con sus enlaces de entrada y sus pesos asignados
se le llama perceptrón. Así la salida del perceptrón tiene un mecanismo para
calcular si está activo en función de los valores dados por la salida de la anterior
capa multiplicados por el peso del enlace de unión.
La función de activación de la neurona es la que define la conversión
de las entradas ponderadas en su activación de salida. Algunas de las funciones
usadas normalmente son: lineal, sigmoidea, escalón, TanH, ReLu
Las redes neuronales se pueden clasificar según su tipología/arquitectura. Algunas
de estas clasificaciones pueden ser las siguientes.
- DNN (Deep Neural Net) la cual tiene más de una capa oculta.
- CNN (Convolutional Neural Net) son especialmente importantes en
el procesamiento de imágenes y la categorización. Se caracterizan por tener capas de filtros convolucionales
que, de manera similar a la corteza visual del cerebro, transforman la entrada
aplicando máscaras para extraer información de distintos tipos. - RNN (Recurrent Neural Net) se caracterizan por tener conexiones recurrentes
con ellas mismas o neuronas de la misma capa. Especialmente interesantes para detección
de patrones, pues permiten «recordar» los valores de la anterior predicción.
Las redes nueronal pueden tener distintos tipos de aprendizaje:
- Aprendizaje supervisado a la red se le proporcionan un conjunto de ejemplos
con sus valores de salida deseados. Así la red se entrena aplicando algoritmos para
ir corrigiendo y propagando los pesos más adecuados para lograr la salida indicada. - Aprendizaje no supervisado solo se le indican entradas a la red sin proporcionarle
los valores de salida correctos/deseados. La red aprende a clasificarlos buscando las
similitudes entre conjuntos de datos - Aprendizaje por refuerzo se enseña al sistema con recompensas o castigos.
Así indicándole el grado de desempeño irá ajustando sus valores para alcanzar el máximo posible
Para ejecutar predicciones y entrenamientos de redes neuronales la mayoría de
operaciones que se realizan son cálculos con matrices. Para el
procesamiento de gráficos una de las tareas más importantes es ésta, por ello el uso de GPUs
en este campo es muy adecuado y puede reducir mucho los tiempos. Google ha dado un
paso más introduciendo unos chips llamados TPUs que están más optimizados y centrados
en los cálculos necesarios para ejecutar algoritmos de aprendizaje automático.
3. TensorFlow
TensorFlow es una herramienta de machine learning. Popularizada por su eficiencia con redes neuronales de aprendizaje profundo pero que
permite la ejecución de procesos distribuidos que no tengan nada que ver con redes neuronales.
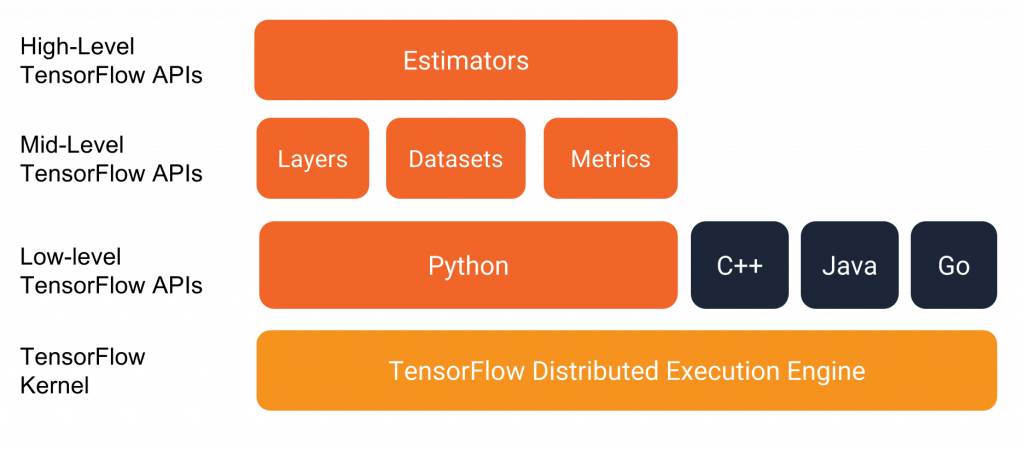
Sus Estimators representan un modelo completo y ofrecen los mecanismos para entrenar los modelos,
evaluar su error y generar predicciónes. Son la capa de más alto nivel.
Te abstraen del entorno donde se ejecutarán ya sea local, un clúster distribuido con CPUs, GPUs o TPUs.
Existen unos «Estimators» predefinidos que facilitan la construcción de redes neuronales sencillas:
- tf.estimator.DNNClassifier para modelos de clasificación con redes profundas.
- tf.estimator.DNNLinearCombinedClassifier para clasificación combinada de modelos lineares y con redes profundas.
- tf.estimator.LinearClassifier para clasificación con modelos lineales.
Otras APIs de alto nivel importantes son:
- Checkpoints: que permiten almacenar y restaurar el estado de configuración de la red.
- Feature columns: para facilitar transformaciones de los datos de entrada mediante intermediarios entre los datos de entrada y los Estimators
- Datasets: herramienta para construir y cargar un input de datos, manipularlo e introducirlo en tu modelo.
- Layers: ofrece una api de alto nivel para la creación de capas de neuronas facilitando sus interconexiones, funciones de activación, etc.
4. Instalando y probando
Lo primero que debemos hacer es instalar TensorFlow. Para ello podemos ver cómo hacerlo según vuestro SO en: https://www.tensorflow.org/install/
En mi caso he optado por la instalación mediante Docker. Ejecutando:
docker run -it gcr.io/tensorflow/tensorflow bash
Esto debería descargar la imagen, crear el docker y arrancarlo. Ahora vamos a probar nuestra instalación. Desde la consola bash de nuestro docker ejecutamos:
python
Ahora en la consola de Python (del propio Docker) introducimos nuestro hola mundo de TensorFlow:
# Python
import tensorflow as tf
hello = tf.constant('Hello, TensorFlow!')
sess = tf.Session()
print(sess.run(hello))
Con la última linea veremos en el output el texto: «Hello, TensorFlow!»
Durante el tutorial arrancaremos el Docker de TensorFlow añadiendo el montaje
de un volumen local para que podamos desde el contenedor de Docker utilizar los ejemplos que
usaremos del repositorio git https://github.com/miyoda/tensorflow-example
docker run -it -v /your-computer-repository-directory:/notebooks/example gcr.io/tensorflow/tensorflow bash
5. Ejemplo visual
En la web https://playground.tensorflow.org
podemos jugar con redes neuronales de una manera muy visual.
Podemos probar para distintos conjuntos de datos diferentes configuraciones de número de capas ocultas, neuronas en cada capa,
función de activación, ratio de aprendizaje, etc.
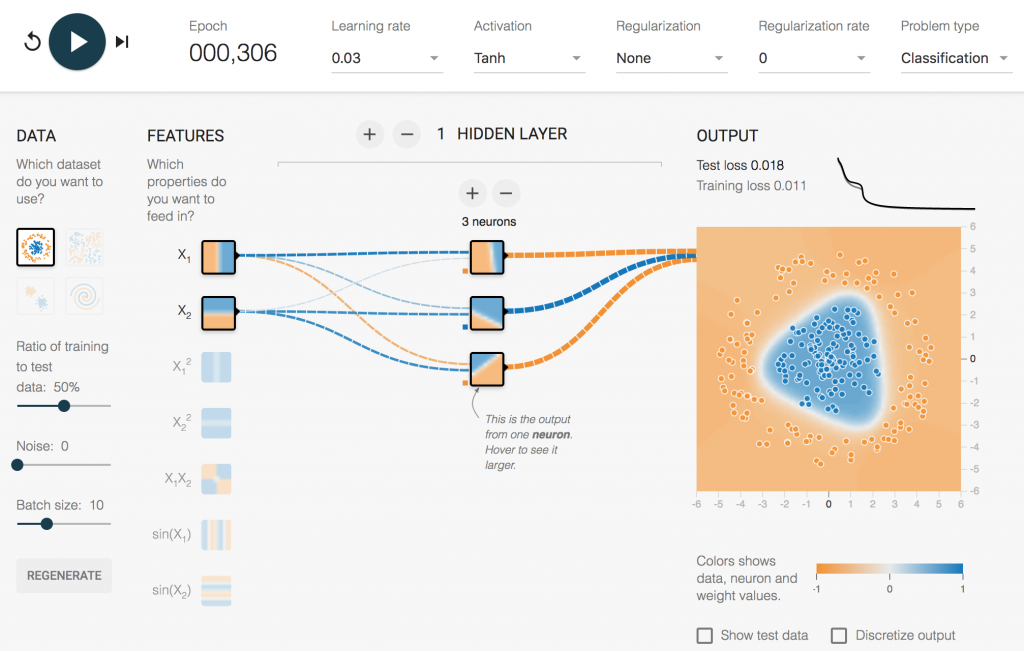
El problema es simplemente categorizar como «Azul» (1) o «Naranja» (-1) un conjunto de puntos que se distribuyen, en función del patrón
de datos indicado a la izquierda, en un sistema de coordenadas cartesianas con «-6 > x > 6» y «-6 > y > 6».
Os animo a que hagáis algunas pruebas y os fijéis sobre todo con el ejemplo básico de datos en «círculo» que vamos a implementar
en Python en el siguiente apartado. Como veréis en este ejemplo se puede lograr una solución con un alto grado de acierto configurando
incluso una sola capa oculta de 3 neuronas y dándole como entrada simplemente los valores de x (X1) e y (X2).
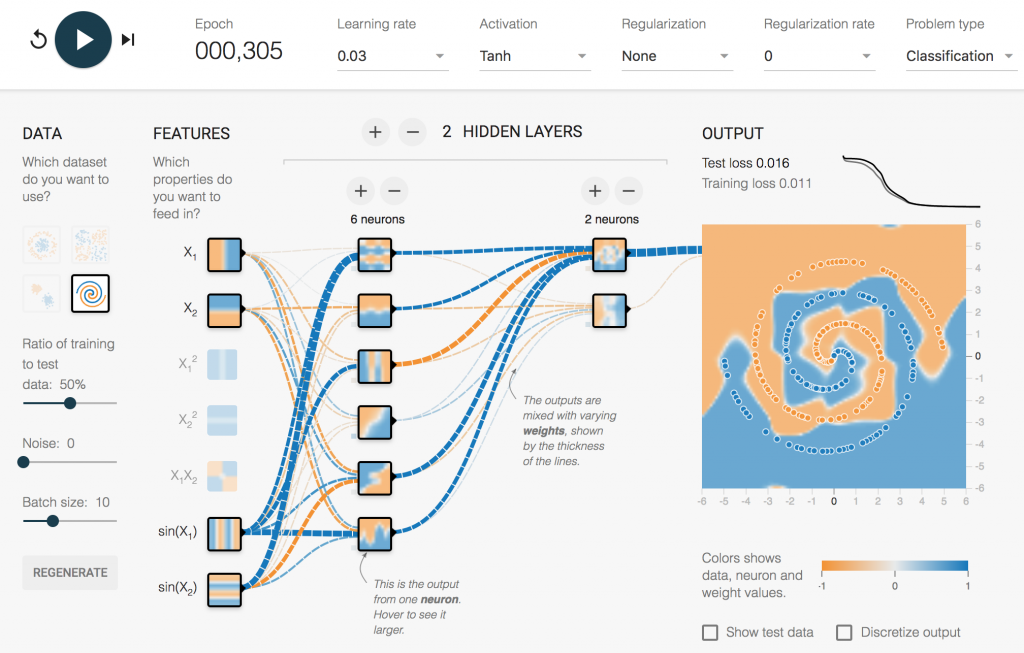
En cambio para solucionar el problema del dataset en «Spiral» la red necesita que le demos información más «precocinada» de los datos.
Así que observaremos que no obtendremos una solución muy buena hasta que no le demos como entrada de la red el cálculo del sen(x) y el sin(y).
Podéis apreciar que la interfaz muestra los enlaces entre las 2 entradas de «sin» mucho más gruesos. Esto es porque han quedado configurados
con mayor peso. Esto no quiere decir que los valores de entrada x e y no sean importantes, pues
de hecho la red no logra una solución buena si quitas estos inputs.
6. Ejemplo en Python
Puedes descargar el código de este ejemplo desde el repositorio https://github.com/miyoda/tensorflow-example
En el subdirectorio «playground-1» tenemos la solución del ejemplo visto anteriormente en la web de playground de TensorFlow.
Lo primero que hemos preparado es un pequeño script para generar los datos de prueba. Esto no tiene mucho sentido si tenemos la «formula» para calcular
los datos clasificados, ¿para qué queremos una red neuronal que nos los clasifique?: Para aprender. Los datos contienen valor de coordenadas del punto (x e y)
y su categorización de color (0 para naranja y 1 para azul). Vamos a verlo en el fichero «data_generator.py»:
import random import math def generate(numPoints): result = [] for i in range(0, numPoints): x = random.uniform(-6,6) y = random.uniform(-6,6) color = 1 if distance((0,0), (x,y)) < 3 else 0 result.append((x,y,color)) return result def distance(pointFrom, pointTo): diff = (pointTo[0] - pointFrom[0], pointTo[1] - pointFrom[1]) return math.sqrt(diff[0]*diff[0]+diff[1]*diff[1])
Por otro lado en el fichero «example_data.py» tenemos algunos métodos para facilitar la preparación de los datos para su uso que
crea conjuntos de datos de entrenamiento (TRAIN) y de prueba (TEST) para que la red pueda entrenarse y autoprobarse durante su etapa
de aprendizaje. Divide los datos a su vez en dos. Los de entrada train_x (coordenadas x e y) y los de salida train_y (color).
Ahora en el fichero «premade_estimator.py» vamos a configurar la red neuronal utilizando un Estimator predefinido. En este caso DDNClassifier.
Lo primero que tenemos que hacer es preparar los datos de entrada y configurar las columnas de input (features):
# Fetch the data
(train_x, train_y), (test_x, test_y) = example_data.load_data()
# Feature columns describe how to use the input.
my_feature_columns = []
for key in train_x.keys():
my_feature_columns.append(tf.feature_column.numeric_column(key=key))
Ahora creamos el Estimator de tipo DNNClassifier indicándole que queremos dos capas ocultas con 6 y 4 neuronas,
y que la clasificación podrá ser entre 2 valores (naranja o azul)
# Build 2 hidden layer DNN with 10, 10 units respectively.
classifier = tf.estimator.DNNClassifier(
feature_columns=my_feature_columns,
# Two hidden layers
hidden_units=[6, 4],
# The model must choose between 2 classes.
n_classes=2)
Procedemos a entrenar el modelo con los datos de entrenamiento generados.
# Train the Model. classifier.train( input_fn=lambda:example_data.train_input_fn(train_x, train_y, args.batch_size), steps=args.train_steps)
Ahora evaluamos la red generada/entrenada con los datos de test. Mostramos por pantalla el «accuracy» el cual tendrá que estar
lo más cerca de 1 posible (dependiendo de las exigencias del problema a resolver).
# Evaluate the model.
eval_result = classifier.evaluate(
input_fn=lambda:example_data.eval_input_fn(test_x, test_y, args.batch_size))
print('\nTest set accuracy: {accuracy:0.3f}\n'.format(**eval_result))
Ahora vamos a utilizar la red ya entrenada con 4 datos de prueba para ver que resultados arroja:
# Generate predictions from the model
expected = ['ORANGE', 'ORANGE', 'BLUE', 'BLUE']
predict_x = {
'x': [-4, -3, 1, -1.5],
'y': [1, -3, -1, 0.5]
}
predictions = classifier.predict(
input_fn=lambda:example_data.eval_input_fn(predict_x,
labels=None,
batch_size=args.batch_size))
template = ('\nPrediction is "{}" ({:.1f}%), expected "{}"')
for pred_dict, expec in zip(predictions, expected):
class_id = pred_dict['class_ids'][0]
probability = pred_dict['probabilities'][class_id]
print(template.format("BLUE" if class_id > 0 else "ORANGE",
100 * probability, expec))
Si ahora arrancamos el Docker de TensorFlow y ejecutamos el código con «python /notebooks/example/playground-1/premade_estimator.py obtendremos algo como lo siguiente:
python /notebooks/example/playground-1/premade_estimator.py
/usr/local/lib/python2.7/dist-packages/h5py/__init__.py:36: FutureWarning: Conversion of the second argument of issubdtype from `float` to `np.floating` is deprecated. In future, it will be treated as `np.float64 == np.dtype(float).type`.
from ._conv import register_converters as _register_converters
TRAIN DATA:
[(3.7930826366632004, 3.0035981747767444, 0), (1.0488879547572427, -5.647917058837368, 0), ...]
TEST DATA:
[(4.669380996775592, 2.339267440220139, 0), (1.7377747136263988, -5.980986206879744, 0), ...]
INFO:tensorflow:Using default config.
WARNING:tensorflow:Using temporary folder as model directory: /tmp/tmp4nrlxU
INFO:tensorflow:Using config: {'_save_checkpoints_secs': 600, '_session_config': None, '_keep_checkpoint_max': 5, '_task_type': 'worker', '_global_id_in_cluster': 0, '_is_chief': True, '_cluster_spec': , '_evaluation_master': '', '_save_checkpoints_steps': None, '_keep_checkpoint_every_n_hours': 10000, '_service': None, '_num_ps_replicas': 0, '_tf_random_seed': None, '_master': '', '_num_worker_replicas': 1, '_task_id': 0, '_log_step_count_steps': 100, '_model_dir': '/tmp/tmp4nrlxU', '_save_summary_steps': 100}
INFO:tensorflow:Calling model_fn.
INFO:tensorflow:Done calling model_fn.
INFO:tensorflow:Create CheckpointSaverHook.
INFO:tensorflow:Graph was finalized.
2018-03-31 09:49:38.236836: I tensorflow/core/platform/cpu_feature_guard.cc:140] Your CPU supports instructions that this TensorFlow binary was not compiled to use: AVX2 FMA
INFO:tensorflow:Running local_init_op.
INFO:tensorflow:Done running local_init_op.
INFO:tensorflow:Saving checkpoints for 1 into /tmp/tmp4nrlxU/model.ckpt.
INFO:tensorflow:loss = 159.065, step = 1
INFO:tensorflow:global_step/sec: 416.865
INFO:tensorflow:loss = 25.40447, step = 101 (0.240 sec)
INFO:tensorflow:global_step/sec: 525.519
INFO:tensorflow:loss = 17.685644, step = 201 (0.190 sec)
INFO:tensorflow:global_step/sec: 537.505
INFO:tensorflow:loss = 14.17207, step = 301 (0.186 sec)
INFO:tensorflow:global_step/sec: 524.442
INFO:tensorflow:loss = 12.54402, step = 401 (0.191 sec)
INFO:tensorflow:global_step/sec: 523.837
INFO:tensorflow:loss = 11.637623, step = 501 (0.191 sec)
INFO:tensorflow:global_step/sec: 531.361
INFO:tensorflow:loss = 8.233404, step = 601 (0.188 sec)
INFO:tensorflow:global_step/sec: 519.661
INFO:tensorflow:loss = 8.66986, step = 701 (0.192 sec)
INFO:tensorflow:global_step/sec: 512.726
INFO:tensorflow:loss = 6.985471, step = 801 (0.195 sec)
INFO:tensorflow:global_step/sec: 517.947
INFO:tensorflow:loss = 6.3264084, step = 901 (0.193 sec)
INFO:tensorflow:Saving checkpoints for 1000 into /tmp/tmp4nrlxU/model.ckpt.
INFO:tensorflow:Loss for final step: 5.9725046.
INFO:tensorflow:Calling model_fn.
INFO:tensorflow:Done calling model_fn.
INFO:tensorflow:Starting evaluation at 2018-03-31-09:49:41
INFO:tensorflow:Graph was finalized.
INFO:tensorflow:Restoring parameters from /tmp/tmp4nrlxU/model.ckpt-1000
INFO:tensorflow:Running local_init_op.
INFO:tensorflow:Done running local_init_op.
INFO:tensorflow:Finished evaluation at 2018-03-31-09:49:41
INFO:tensorflow:Saving dict for global step 1000: accuracy = 0.975, accuracy_baseline = 0.825, auc = 0.99278504, auc_precision_recall = 0.9732998, average_loss = 0.095491454, global_step = 1000, label/mean = 0.175, loss = 5.7294874, prediction/mean = 0.15055662
Test set accuracy: 0.975
INFO:tensorflow:Calling model_fn.
INFO:tensorflow:Done calling model_fn.
INFO:tensorflow:Graph was finalized.
INFO:tensorflow:Restoring parameters from /tmp/tmp4nrlxU/model.ckpt-1000
INFO:tensorflow:Running local_init_op.
INFO:tensorflow:Done running local_init_op.
{'probabilities': array([0.9810508 , 0.01894918], dtype=float32), 'logits': array([-3.9468637], dtype=float32), 'classes': array(['0'], dtype=object), 'class_ids': array([0]), 'logistic': array([0.01894918], dtype=float32)}
Prediction is "ORANGE" (98.1%), expected "ORANGE"
{'probabilities': array([0.9895298 , 0.01047021], dtype=float32), 'logits': array([-4.5486956], dtype=float32), 'classes': array(['0'], dtype=object), 'class_ids': array([0]), 'logistic': array([0.01047021], dtype=float32)}
Prediction is "ORANGE" (99.0%), expected "ORANGE"
{'probabilities': array([0.15968752, 0.84031254], dtype=float32), 'logits': array([1.660555], dtype=float32), 'classes': array(['1'], dtype=object), 'class_ids': array([1]), 'logistic': array([0.84031254], dtype=float32)}
Prediction is "BLUE" (84.0%), expected "BLUE"
{'probabilities': array([0.15968752, 0.84031254], dtype=float32), 'logits': array([1.660555], dtype=float32), 'classes': array(['1'], dtype=object), 'class_ids': array([1]), 'logistic': array([0.84031254], dtype=float32)}
Prediction is "BLUE" (84.0%), expected "BLUE"
Podemos ver que hemos obtenido un «accuracy» de 0.975 y que parece que funciona bastante bien con las predicciones solicitadas.
7. Referencias
8. Conclusiones
Como hemos visto TensorFlow nos facilita mucho la construcción de redes neuronales complejas.
Y lo más importante es que está preparado para escalar la solución y optimizar su ejecución
en arquitecturas distribuidas sobre GPUs que aumentan increiblemente su eficiencia.




Muy interesante, Miguel
Hellow my name is MartinDeabs. Wery good art! Thx 🙂