Descomposición factorial de 32597 y la lotería de navidad

El año pasado compré por primera vez lotería. El número 32597. Lo vi y me pareció especial. ¿Pero cómo de especial es?. En este artículo, usaremos javascript para responder a ciertas preguntas sobre el número 32597 y encontraremos un algoritmo para hacer la descomposición factorial en números primos de cualquier número.

Índice de contenidos

• 1. Introducción
• 2. Pero ¿cómo de especial es el número 32597?
• 3. Números primos menores que 100000
• 4. Descomposición factorial de un número
• 5. La importancia del rendimiento
• 6. Estrategias orientadas al rendimiento
• 7. Descomposición factorial de un número
• 8. Descomposición factorial de todos los números hasta el 100.000K
• 9. ¿Y cuántos semiprimos hay?
• 10. ¿Y los cuadrados perfectos de primos?
• 11. Conclusiones

1. Introducción.

No compro lotería. Ningún tipo de lotería. Y no me gustan los juegos de azar. No siento la emoción al girar la ruleta y ver que me puede tocar, ni las tragaperras, ni tampoco la lotería. Los que juegan a mi alrededor no tienen ninguna patología, ni son ludópatas. Compran con ilusión. Y digo «compran», donde otros dicen «juegan», porque para mi la palabra jugar tiene un componente lúdico, y aunque pueda intervenir el azar, al menos puedes desarrollar estrategias más o menos acertadas para ganar a tus adversarios. Sin embargo, no siento eso con la lotería. Es azar puro. Me aburre, y me parece tirar el dinero.

Pero el año pasado contravine mis propias reglas. Y este artículo es la penitencia por ello. Estaba yo en la barra de un bar, lugar donde se fraguan las mejores historias y que yo frecuento con regocijo acompañado de amigos, cuando vi que tras el mostrador exponían el número 32597 de la lotería de Navidad. ¡Pardiez! En seguida me di cuenta que ese número era 37 x 881, dos números primos. Sí, lo sé, mi mente con frecuencia me lleva por senderos poco transitados.

El caso, es que detectar ese hecho lo consideré una señal. Probablemente mi lóbulo temporal derecho tenga la culpa de esa creencia. Acto seguido me encontré comprando el número y contándole esta historia al barman, que me miraba con cara extraña mientras secaba un vaso.

Y llegó el día, y claro, pasó lo que tenía que pasar: ¡No me tocó!

2. Pero ¿cómo de especial es el número 32597?

Sabía que era múltiplo de 37 porque recuerdo un tipo que ganó Cifras y Letras porque se sabía el criterio de divisibilidad del 37. Saberlo ya es raro, y poderlo aplicar en un programa de la televisión lo es más. Tenía que aprender aquella maravilla. Y así fue como leí sobre aquello.

Y el 881 ya sabía que era primo. De pequeño aprendí los primos menores de 1000, y lo que aprendo una vez no suelo olvidarlo nunca. Así fue como reconocí el producto de esos dos números casi al instante.

La pregunta es ¿cuantos números menores de 100.000 son el producto de dos números primos?

Gracias a Dios no estamos en tiempos de Erastótenes, y hoy disponemos de ordenadores. Cuando me hice esta pregunta acudí a una herramienta muy potente que me permite probar cosas muy rápido: la consola del navegador. Puedo hacer programitas, y que me dé los resultados de forma rápida.

Vamos a ello, pero además, vamos a intentar prestar atención al rendimiento.

3. Números primos menores que 100000

El objetivo es obtener un array con los números primos menores que 100000.

Pero ¿como sabemos que un número es primo?
Si lo dividimos por todos los números menores que él y mayores que 1 y ninguno da resto cero ¿no?

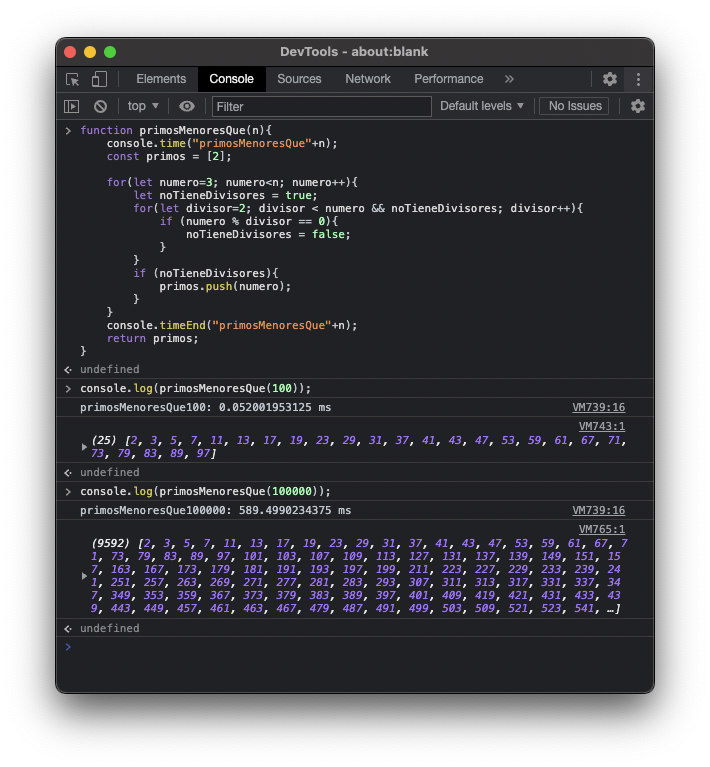
function primosMenoresQue(n){
    console.time("primosMenoresQue"+n);
    const primos = [2];

    for(let numero=3; numero<n; numero++){
        let noTieneDivisores = true;
        for(let divisor=2; divisor < numero && noTieneDivisores; divisor++){
            if (numero % divisor == 0){
                noTieneDivisores = false;
            }
        }
        if (noTieneDivisores){
            primos.push(numero);
        }
    }
    console.timeEnd("primosMenoresQue"+n);
    return primos;
}

Pero nosotros valemos más que eso ¿no? Realmente sabemos que un número es primo si no es divisible por los primos anteriores a él.
En el algoritmo anterior estamos dividiendo por muchos más números. Vamos con la versión 2.

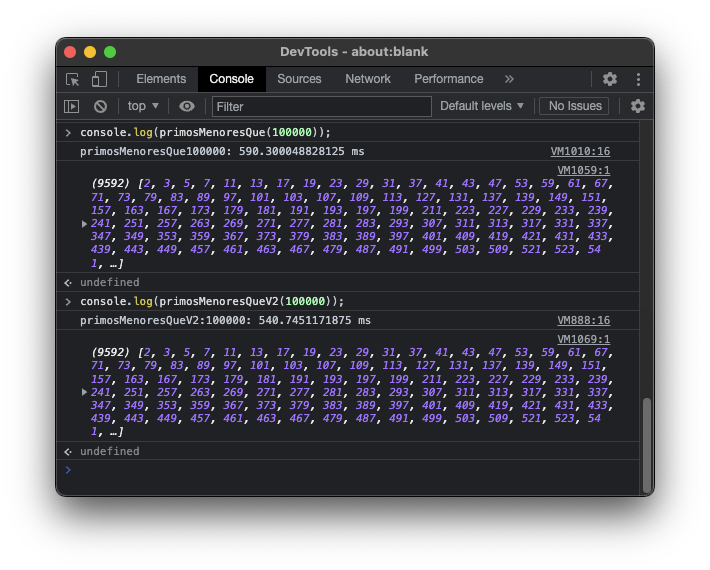
function primosMenoresQueV2(n){
    console.time("primosMenoresQueV2:"+n);
    const primos = [2];

    for(let numero=3; numero < n; numero++){
        let noTieneDivisores = true;
        primos.forEach(divisor => {
            if (numero % divisor == 0){
                noTieneDivisores = false;
            }
        })
        if (noTieneDivisores){
            primos.push(numero);
        }
    }
    console.timeEnd("primosMenoresQueV2:"+n);
    return primos;
}

Pues a pesar de hacer muchas menos operaciones, tampoco hemos ganado mucho. Apenas 50 milisegundos

Vamos a ver qué podemos hacer para seguir optimizando. Me doy cuenta que para saber si un número es primo, no tenemos que dividir por todos los primos hasta llegar a él. Una primera aproximación, sería recorrer sólo hasta la mitad ¿no? Pues cada vez que encuentras un divisor menor que la mitad encuentras otro mayor que la mitad. Pero es que siguiendo ese mismo razonamiento, puedes aplicarlo sólo hasta la raíz cuadrada del número. Y ahí descartamos mucho más rápido.

En este vídeo explican visualmente muy bien porque es suficiente con comprobar hasta la raíz cuadrada. Así que vamos con la versión 3. A ver si mejoramos algo.

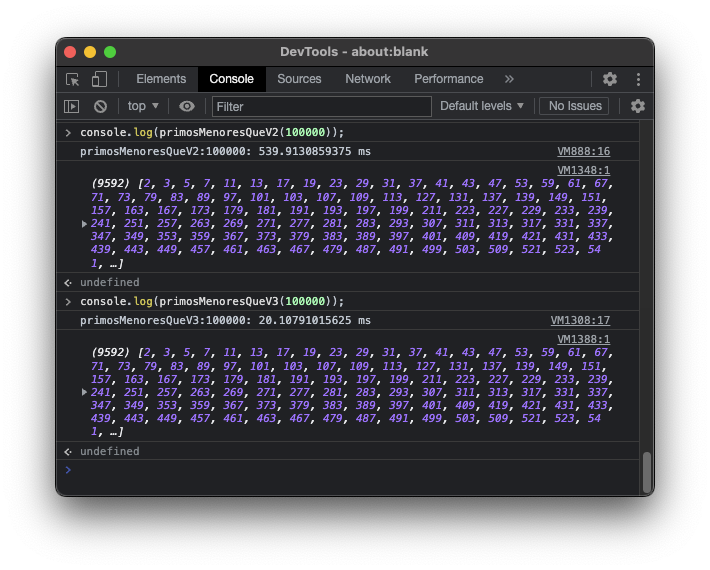
function primosMenoresQueV3(n){
    console.time("primosMenoresQueV3:"+n);
    const primos = [2];

    for(let numero=3; numero<n; numero++){
        let noTieneDivisores = true;
        const MAX = Math.sqrt(numero)
        for (let i=0; i<primos.length && primos[i] <= MAX; i++){
            if (numero % primos[i] == 0){
                noTieneDivisores = false;
            }
        }
        if (noTieneDivisores){
            primos.push(numero);
        }
    }
    console.timeEnd("primosMenoresQueV3:"+n);
    return primos;
}

¡Este sí que es eficaz! Hemos pasado de 539ms a 20ms

¿Se os ocurre algo para mejorarlo? A mi ya se me están acabando las ideas. Se me ha ocurrido una muy chorra. Y es que sé que a partir del 3 todos los primos son de la forma 6n-1 o 6n+1. Con esto descartamos 4 de cada 6 números, teniendo sólo dos candidatos de cada seis. De esta forma recorreríamos mucho más rápido al reducir el número de candidatos. Y además podemos ir de dos en dos, pues los pares mayores que 2 sabemos que no son primos. Vamos con la versión 4, aunque yo creo que ya no hay mucho margen de mejora.

Que p sea de la forma 6n-1 o 6n+1 ==> (p+1) mod 6 == 0 o que (p-1) mod 6 == 0

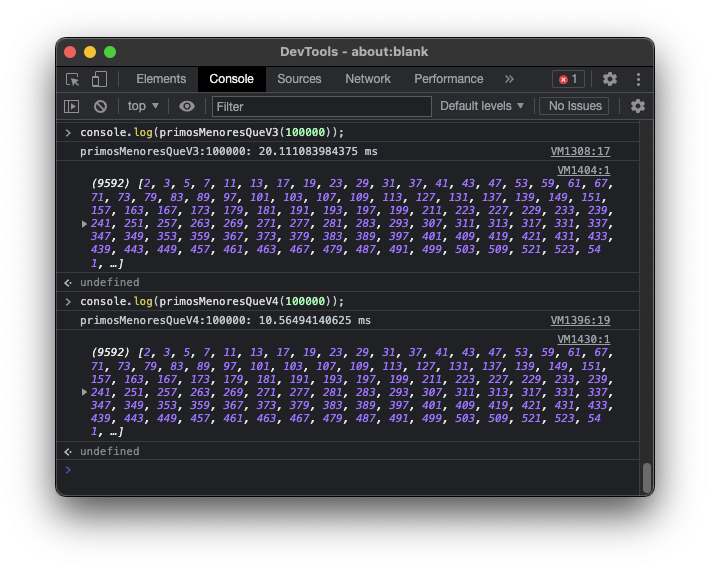
function primosMenoresQueV4(n){
    console.time("primosMenoresQueV4:"+n);
    const primos = [2,3];

    for(let numero=5; numero<n; numero = numero + 2){
        if ( (numero+1)%6 == 0 || (numero-1)%6 == 0) {
            let noTieneDivisores = true;
            const MAX = Math.sqrt(numero)
            for (let i=0; i<primos.length && primos[i] <= MAX; i++){
                if (numero % primos[i] == 0){
                    noTieneDivisores = false;
                }
            }
            if (noTieneDivisores){
                primos.push(numero);
            }
        }
    }
    console.timeEnd("primosMenoresQueV4:"+n);
    return primos;
}

Pues oye, sí, lo hemos reducido otra vez a la mitad: 10 milisegundos.

5. La importancia del rendimiento

Muchas veces no somos conscientes de lo que implica el rendimiento. Y en el mundo empresarial, no siempre se le da la importancia que debiera tener. En este ejemplo estamos circunscritos a los números de lotería, pero ¿y si no fuera así? ¿hasta donde podríamos llegar con estos algoritmos?

Vamos a ver un ejemplo con 10⁷: un 1 seguido de 7 ceros… Y vamos a comparar cuánto tardan estos algoritmos en calcular todos los números primos hasta 10⁷.

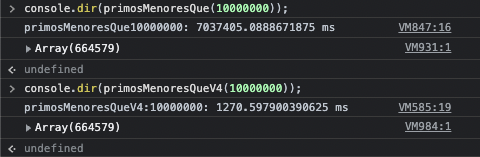
Con la V1 es casi imposible obtener los primos menores que 10⁷. La diferencia entre V1 y V4 se hace evidente para este cifra

• V1 tarda ~7037″ en calcularlo = 1h 57′ 17″
• V4 tarda ~1″ en calcularlo = 1 segundo

Me sigue alucinando el tema de la optimización. En un mundo en el que se paga por ciclos de CPU, no optimizar, es derrochar… es tirar dinero a la basura. Y da igual si hablas de queries, de microservicios o de lo que sea… es una cuestión de pasta. Mucho dinero.

Por no decir que V1 te imposibilita ir más allá de 10⁷ mientras que con V4 podemos llegar más lejos… pero ¿cuánto más lejos?
Venga, va, vamos a hacer el burro…

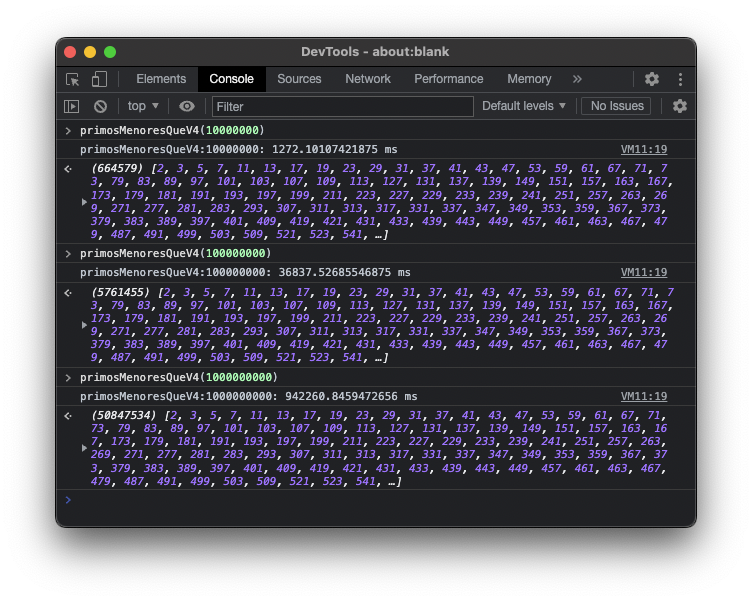
Ya con 10⁹ se le empieza a hacer bola. Parece difícil que con esta versión podamos ir mucho más allá.

• V4 con 10⁷ tarda ~1″
• V4 con 10⁸ tarda ~37″
• V4 con 10⁹ tarda ~942″

6. Estrategias orientadas al rendimiento

Podemos hacer muchas refactorizaciones de nuestro código. Lo más probable es que en cada iteración, pensemos en hacer nuestro código más simple. Más legible. Pero cuando pensamos en rendimiento ¿cuál es la estrategia acertada? ¿qué podemos hacer para mejorar el rendimiento de nuestro programa?

Mi mente, sin querer, me exige buscar siempre el mayor rendimiento posible y los caminos que exploro suelen ser los siguientes:

• reducir cardinalidades: da igual si se trata de hacer dos JOINs de una query o recorrer candidatos en un proceso iterativo. Siempre que se pueda, reduce la cardinalidad de lo que quieres tratar. En el ejemplo que llevamos hemos reducido cardinalidad llegando sólo hasta la raíz cuadrada del número.
• descarta rápido, descarta fácil: sabemos que los pares mayor que dos no son primos, podemos descartalos fácil, pero contraviene la primera regla. Es más barato sacarlos del grupo de candidatos reduciendo la cardinalidad, que hacer la comprobación de si es par y descartarlo. Por ejemplo, en V4 estamos comprobando si el número es múltiplo de 6 menos 1 o múltiplo de 6 mas 1… ¿No habría sido mejor reducir la cardinalidad a estos candidados y no hacer las comprobaciones?
• no proceses de más: muchas veces procesamos información redundante. Y a esto nos ayuda a darnos cuenta las pequeñas refactorizaciones.

Ya V4 parece poco mejorable, por lo que hemos podido ver, pero es verdad que el código ha quedado menos legible que la V1. Vamos a aprovechar para refactorizar y hacerlo más legible y vamos a intentar seguir estas estrategias.

Lo primero que nos damos cuenta es que estamos recorriendo los números de dos en dos, los impares, y luego comprobando si son de la forma 6n-1 o 6n+1. ¿No sería más eficaz recorrer de 6 en 6 y ver si el número anterior y posterior son primos? 5 y 7, 9 y 11, 17 y 19, 23 y 25, etc… Recorremos más deprisa, y hacemos menos comprobaciones.

6.1 Vamos con la V5

function primosMenoresQueV5(n){
    console.time("primosMenoresQueV5:"+n);
    const primos = [2,3];

    for(let numero=6; numero<n; numero = numero + 6){
        //candidato de la forma 6n-1
        (
            const candidato = numero - 1;
            let noTieneDivisores = true;
            const MAX = Math.sqrt(candidato)
            for (let i=0; i<primos.length && primos[i] <= MAX; i++){
                if (candidato % primos[i] == 0){
                    noTieneDivisores = false;
                }
            }
            if (noTieneDivisores){
                primos.push(candidato);
            }
        )
        
        //candidato de la forma 6n+1
        (
            const candidato = numero + 1;
            let noTieneDivisores = true;
            const MAX = Math.sqrt(candidato)
            for (let i=0; i<primos.length && primos[i] <= MAX; i++){
                if (candidato % primos[i] == 0){
                    noTieneDivisores = false;
                }
            }
            if (noTieneDivisores){
                primos.push(candidato);
            }
        )

    }
    console.timeEnd("primosMenoresQueV5:"+n);
    return primos;
}

Pero claro, nos ha quedado un poco feo… identificamos un bloque que se repite dos veces, que calcula si tiene o no tiene divisores el candidato. Es susceptible de extraerlo factor común y refactorizarlo a una función…

function noTieneDivisores(candidato, primos){
    let noTieneDivisores = true;
    const MAX = Math.sqrt(candidato)
    for (let i=0; i<primos.length && primos[i] <= MAX; i++){
        if (candidato % primos[i] == 0){
            noTieneDivisores = false;
        }
    }
    return noTieneDivisores;
}

function primosMenoresQueV5(n){
    console.time("primosMenoresQueV5:"+n);
    const primos = [2,3];

    for(let numero=6; numero<n; numero = numero + 6){
        
        if (noTieneDivisores(numero-1, primos)){
            primos.push(numero-1);
        }
    
        if (noTieneDivisores(numero+1, primos)){
            primos.push(numero+1);
        }
    }
    console.timeEnd("primosMenoresQueV5:"+n);
    return primos;
}

6.2 Siguiente iteración

Esto va quedando más simple, pero fijémonos en la función noTieneDivisores(candidato, primos). Lo primero es que no es buena idea pensar en negativo. Sería preferible ver si tiene divisores, a ver si no tiene divisores ¿no?. Por otro lado, si encontramos un divisor, ya es suficiente para saber que tiene divisores. No tendríamos porque seguir comprobando hasta el final.

Propongo parar y salir del bucle en el momento en que encontremos un divisor.

function tieneDivisores(candidato, primos){
    let tieneDivisores = false;
    const MAX = Math.sqrt(candidato)
    for (let i=0; i<primos.length && primos[i] <= MAX; i++){
        if (candidato % primos[i] == 0){
            tieneDivisores = true;
            break;
        }
    }
    return tieneDivisores;
}

function primosMenoresQueV5(n){
    console.time("primosMenoresQueV5:"+n);
    const primos = [2,3];

    for(let numero=6; numero<n; numero = numero + 6){
        if (!tieneDivisores(numero - 1, primos)){
            primos.push(numero-1);
        }
        if (!tieneDivisores(numero + 1, primos)){
            primos.push(numero+1);
        }        
    }
    console.timeEnd("primosMenoresQueV5:"+n);
    return primos;
}

Y creo que sí, que ahora ya sí que hemos aumentado la legibilidad y además hemos mejorado. Vamos a ver cuánto.

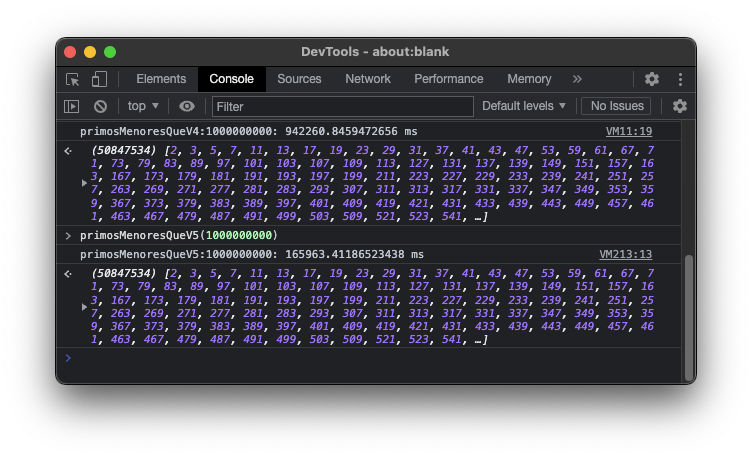
Hemos pasado de calcular los primos menores de 10⁹:

• con V4 en 942″ = ~15′ 42″
• con V5 en 166″ = ~2′ 46″

Ya estamos abriendo la puerta a calcular los primos menores a 10¹⁰;

Ahora tenemos ordenadores muy potentes, y como obtenemos resultados en tiempos razonables, cada vez se le presta menos atención al rendimiento, pero no es algo baladí, que se deba perder de vista. No tenerlo en cuenta es derrochar recursos, tiempo, y dinero. Mucho dinero.

Continuemos con el problema de la lotería que nos había traído hasta aquí.

7. Descomposición factorial de un número

Vamos a buscar un algoritmo eficaz para hacer la descomposición factorial.

const primos = primosMenoresQue(100000);

function despomposicionFactorial(n) {
    const descFactorial = new Map();
    let dividendo = n;
    let contPrimos = 0;
    let divisor = primos[contPrimos];

    while (dividendo > 1) {
        if (dividendo % divisor == 0){
        	if (descFactorial.has(divisor)){
        		let exponente = descFactorial.get(divisor) + 1;
        		descFactorial.set(divisor, exponente);
        	} else {
        		descFactorial.set(divisor, 1);
        	}
        	dividendo = dividendo / divisor;
        } else {
            contPrimos++
        	divisor = primos[contPrimos];
        }
    }
    return descFactorial;
}

Probamos que efectivamente funciona y nos da resultados en tiempos óptimos. Y vamos con lo siguiente, que sería descomponer cada uno de los números del 1 hasta el 99999

8. Descomposición factorial de todos los números hasta 100000

Básicamente, sería juntar todo, y guardar el resultado en una constante:

function descomposicionFactorialMenoresQue(n) {
    const descFactMenores = new Array(n)

    for (let i = 1; i<n; i++){
        descFactMenores[i] = despomposicionFactorial(i);
    }

    return descFactMenores;
}

const menoresQue100k = descomposicionFactorialMenoresQue(100000);

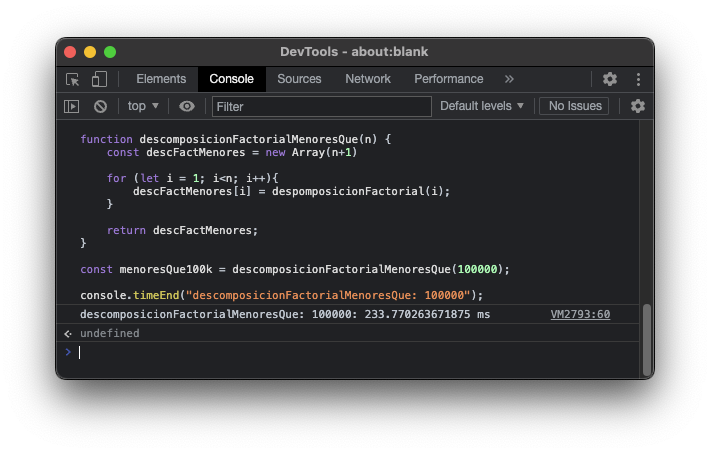
Bien, nos lo ha calculado en total en 233 ms

9. ¿Y cuántos semiprimos hay?

Ya vimos que 32597 es el producto de dos primos. A ese tipo de números se les llama semiprimos o biprimos.

Habría que contar los elementos del array menoresQue100k que se pueden factorizar en dos bases y sendos exponentes son 1.

let semiPrimos = [];
for (let i = 2; i < menoresQue100k.length; i++){
    if (menoresQue100k[i].size == 2){
        const candidato = menoresQue100k[i];
        let esSemiPrimo = true;
        for (let base of candidato.keys()){
            let exponente = candidato.get(base);
            if (exponente > 1){
                esSemiPrimo = false;
            }
        }
        if (esSemiPrimo){
            semiPrimos.push(candidato);
        }
    }
}

console.log("hay excatamente %s semiprimos", semiPrimos.length);

Pues no. Mi número no es nada especial. Hay 23.313 semiprimos entre los 100.000 primeros números naturales. Casi la cuarta parte.

10. ¿Y los cuadrados perfectos de primos?

También son semiprimos ¿no?

Esos sólo tendrían una base, pero su exponente sería 2

let cuadradosPerfecto = [];
for (let i = 2; i < menoresQue100k.length; i++){
    if (menoresQue100k[i].size == 1){
        const candidato = menoresQue100k[i];
        let esCuadradoPerfecto = true;
        for (let base of candidato.keys()){
            let exponente = candidato.get(base);
            if (exponente != 2){
                esCuadradoPerfecto = false;
            }
        }
        if (esCuadradoPerfecto){
            cuadradosPerfecto.push(candidato);
        }
    }
}

console.log("hay excatamente %s cuadrados perfectos", cuadradosPerfecto.length);

Hay exactamente 65 cuadrados perfectos.

11. Conclusiones

He pagado gustoso mi penitencia de comprar lotería el año pasado. Me lo he pasado muy bien haciéndome estas cuestiones.

He refrescado varias cosas:

• que la lotería de navidad cuesta ¡20 euros!
• que el sorteo es el día 22 de diciembre
• y que da igual las señales que recibas, que todos los números tienen las mismas probabilidades
• que no hay números especiales

Y espero que tú, lector, hayas aprendido algunas otras cosas:

• de la importancia del rendimiento en cualquier sistema
• que la refactorización es el camino
• y que es una forma de pensar que hay que interiorizar

En caso de que esta forma de pensar haya calado en ti, la hayas interiorizado, y hayas seguido el resto del artículo con interés y atención, seguro que te habrás dado cuenta que cuando hago la descomposición factorial de un número, tras la primera división, no aprovecho que probablemente ya tengo calculada la descomposición factorial del cociente, y la vuelvo a calcular iterativamente.

¿Te has dado cuenta? ¡Enhorabuena!, tienes la cabeza muy bien amueblada para esto del rendimiento.
Si no te has dado cuenta, no desistas. No era fácil de ver. Esto es un cambio de forma de pensar que se va adquiriendo poco a poco.

Si te ha gustado este tipo de problemas de programación, te recomiendo el Proyecto Euler. Son problemas de este estilo, y requieren pararse a pensar. Puedes elegir el lenguaje de programación que más te guste, y así practicar.